EmbVision チュートリアル（２）

フィルタリングと周波数特性

新潟大学　工学部　電気電子工学科　村松　正吾

一次元信号の周波数特性
一次元信号のフィルタリング
一次元フィルタの周波数応答
二次元信号の周波数特性
二次元信号のフィルタリング
二次元フィルタの周波数応答
演習課題

概要

本演習では、MATLABにて一次元信号のフィルタリングと周波数解析法、画像情報のフィルタリングと周波数解析法について簡単に学ぶ。

準備として、開いている全ての Figure を close 関数で閉じておく。

close all

一次元信号の周波数特性

まず、予め用意されているオーディオデータ chirp を load 関数を利用して読み出して準備する。

load chirp

オーディオデータは変数 y に倍精度実数型配列として保持される。なお、標本化周波数は変数 Fs に保持される。

whos y Fs

  Name          Size             Bytes  Class     Attributes

  Fs            1x1                  8  double              
  y         13129x1             105032  double

次に、予め用意されているオーディオデータ gong を読み出し、 length 関数を利用して長さを揃え、 chirp のデータと混合する。

c = y; % 変数 c に代入
load gong
g = y; % 変数 g に代入

x = g(1:length(c))+c; % 長さを調整して混合

変数 x には混合したオーディオデータが保持される。 plot 関数で確認しよう。

plot(x)

オーディオ再生環境があれば audioplayer 関数を利用して、オーディオ再生も可能である。

まず、オーディオ再生オブジェクトを生成する。

player = audioplayer(x,Fs);
whos player

オーディオ再生は、 play メソッドにオブジェクト player を指定して実行される。

play(player)

spectrogram 関数を利用することで、短時間フーリエ変換を利用したオーディオデータの周波数解析を実行できる。

窓長: 256

として実行しよう。

figure(1)
spectrogram(x,256)
caxis([ -70 10 ])
colorbar

上記の操作により周波数特性（スペクトログラム）が表示される。横軸は正規化周波数( 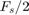$$ F_s/2 $$ を 1 と正規化)、縦軸は標本インデックス( 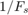$$ 1/F_s $$ 秒単位)である。

なお、値の大きさ[dB] が分かり易いように caxis 関数と colorbar 関数を併用した。

view 関数で視点を変えてみよう。

view([-15 30])

zlim 関数を利用して、 Z軸の座標を　-70 から 10 に調整する。

zlim([ -70 10 ])

[ トップ ]

一次元信号のフィルタリング

次に、オーディオデータ x に、線形フィルタ処理

$y[n] = h[n] \ast x[n] = \sum_{k=0}^{N-1} h[k]x[n-k]$

を施してみよう。ここで、

: フィルタ入力
: フィルタ出力
: フィルタ係数（インパルス応答）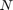
: フィルタ次数

とする。

MATLAB では線形フィルタ処理に conv 関数を利用できる。

フィルタ係数

$h[n] = \left\{\begin{array}{ll} 1/3, & n=0,1,2 \\ 0, & \mathrm{otherwise} \end{array}\right.$

として線形フィルタ処理を実行してみよう。

h = [ 1 1 1 ]/3;
figure(2)
impz(h)

y = conv(h,x);

変数 y にはフィルタ処理結果が保持されている。出力 y の周波数特性（スペクトログラム）を確認しよう。

figure(3)
spectrogram(y,256);
caxis([ -70 10 ])
colorbar

view([ -15 30 ])
zlim([ -70 10 ])

入力 x と出力 y のスペクトログラムを比較してみて欲しい。どのようなことに気が付くだろうか？

大よそ、正規化周波数0.4以上の高周波成分が減衰している。
特に、0.667付近の減衰が大きい。

ということに注意して観察して欲しい。

なお、処理結果をオーディオ再生により確認する場合は、

player = audioplayer(y,Fs);
play(player)

と実行すればよい。

[ トップ ]

一次元フィルタの周波数応答

線形フィルタによる周波数特性の変化は、フィルタの周波数応答により確認できる。

何故ならば、時間領域での畳込み演算は

$y[n] = h[n] \ast x[n] \ \stackrel{\mathrm{DTFT}}{\longleftrightarrow}\ Y(e^{j\omega}) = H(e^{j\omega})X(e^{j\omega})$

のように周波数（DTFT: 離散時間フーリエ変換）領域では積演算に対応するためである。ここで、

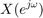$X(e^{j\omega})$ : 入力の周波数特性
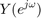$Y(e^{j\omega})$ : 出力の周波数特性
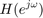$H(e^{j\omega})$ : フィルタ係数（インパルス応答）の周波数応答

である。

フィルタ係数 $$ h[n] $$ の周波数応答は freqz 関数により確認できる。

figure(4)
freqz(h)

振幅応答を確認すると、正規化周波数 0.3 から　0.4 の間から高域に渡り -6 [dB] 以上の減衰特性をもち、特に 0.6 から 0.7 の間で大きく減衰する特性が確認できる。

なお、

$H(e^{j\omega}) = \sum_{n=-\infty}^{\infty} h[n]e^{-j\omega n} = h[0]e^{-j0} + h[1]e^{-j\omega} + h[2]e^{-j2\omega}$

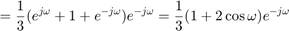
$= \frac{1}{3}(e^{j\omega} + 1 + e^{-j\omega})e^{-j\omega} = \frac{1}{3}(1 + 2\cos\omega)e^{-j\omega}$

より、

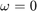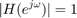
$\omega = 0$ で、 $|H(e^{j\omega})| = 1$
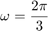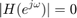
$\omega = \frac{2\pi}{3}$ で、 $|H(e^{j\omega})| = 0$

となることが確認できる。

[ トップ ]

二次元信号の周波数特性

では、画像データに対するフィルタリングに話を進めよう。先に示したオーディオデータと同様に線形フィルタ処理を施すことができる。

まず、開いている全ての Figure を close 関数でで閉じた後、予め用意されている画像データ cameraman を読み込んで表示しよう。

close all
figure(1)
X = imread('cameraman.tif');
imshow(X)

画像データは変数 X に符号なし整数８ビット型配列として保持されるので、これを倍精度実数型に変換しよう。

X = im2double(X);
whos X

  Name        Size              Bytes  Class     Attributes

  X         256x256            524288  double

fft2 関数を利用することで、画像データの二次元の周波数解析を実行できる。画像サイズに合わせて

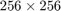
二次元FFT点数: $256\times 256$

と設定し二次元周波数解析を実行しよう。

F = fft2(X,256,256);
whos F

  Name        Size               Bytes  Class     Attributes

  F         256x256            1048576  double    complex

変数 F に二次元離散フーリエ変換(DFT)係数が保持される。なお、複素数として結果が得られるため、絶対値をとって振幅特性を求めてみよう。

Fmag = abs(F);
whos Fmag

  Name        Size              Bytes  Class     Attributes

  Fmag      256x256            524288  double

変数 Fmag には、振幅特性として実数配列が保持される。 surface 関数を利用して、特性を可視化しよう。

surface プロットを調整するためのハンドルオブジェクトとして変数 hsrfc を用意しておこう。

figure(2)
hsrfc = surface(20*log10(Fmag));
set(hsrfc,'EdgeColor','none');

ここでは、デシベルに換算している点に注意する。

グラフが見やすいようカラーバーを設置する。

colorbar
caxis([ -20 80 ])

中心が直流となるように fftshift 関数を用いて配列をシフトする。

set(hsrfc,'ZData',fftshift(hsrfc.ZData)); % Z軸のシフト
set(hsrfc,'CData',fftshift(hsrfc.CData)); % カラー軸のシフト

正規化周波数となるよう座標の調整を行う。

fstep = 1/256; % 周波数標本点の間隔
set(hsrfc,'XData',-0.5:fstep:0.5-fstep);
set(hsrfc,'YData',-0.5:fstep:0.5-fstep);
xlabel('F_x (\times\pi rad/sample)')
ylabel('F_y (\times\pi rad/sample)')

視点を変える。

view([ -15 30 ])
zlim([ -20 80 ])

[ トップ ]

二次元信号のフィルタリング

次に、画像データ X に、二次元線形フィルタ処理

$y[n_y,n_x] = h[n_y,n_x] \ast x[n_y,n_x] = \sum_{k_x=0}^{N_x-1}\sum_{k_y=0}^{N_y-1} h[k_y,k_x]x[n_y-k_y,n_x-k_x]$

を施してみよう。ここで、

: フィルタ入力
: フィルタ出力
: フィルタ係数（インパルス応答）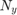
: 垂直フィルタ次数
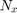: 水平フィルタ次数

とする。

MATLAB では二次元線形フィルタ処理に conv2 関数もしくは imfilter 関数を利用できる。

フィルタ係数 $$ h[n_y,n_x] $$ として配列

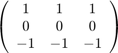
$\left(\begin{array}{ccc} 1 & 1 & 1 \\ 0 & 0 & 0 \\ -1 & -1 & -1 \\ \end{array}\right)$

を利用して線形フィルタ処理を実行してみよう。

H = [ 1 1 1 ; 0 0 0 ; -1 -1 -1 ];
Y = conv2(H,X);

変数 Y にはフィルタ処理結果が保持されている。ただし、

size(Y)

ans =

   258   258

のように、もとの配列 X よりもサイズが縦横 2 画素づつ増加している。これは、サイズ 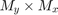$M_y\times M_x$ の画像にサイズ 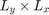$L_y\times L_x$ の線形フィルタをかけるとその出力のサイズが

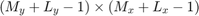
$(M_y+L_y-1)\times (M_x+L_x-1)$

に増加する性質による。

上下左右、1画素ずつ削って、入力画像 X のサイズに出力画像 Y のサイズを調整しよう。 end 関数を利用した配列インデックスの最大値指定を利用すると便利である。

Y = Y(2:end-1,2:end-1);

また、出力画像 Y は、演算の結果、

min(Y(:))

ans =

   -2.7882

のように、負の値を含む。このため画像として表示する際には工夫が必要である。

実数型画像の場合、imshow 関数は、画素値が 0 から 1 にスケールされていると仮定して表示を行うので、負の値が0.5 以下、正の値が0.5以上となるよう Y の値を調整する。

figure(3)
imshow(Y+0.5)

先のフィルタは、垂直方向の微分 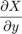$\frac{\partial X}{\partial y}$ の離散近似を出力する。

出力 Y の周波数特性を確認しよう。

figure(4)
F = fft2(Y,256,256);
Fmag = abs(F);
hsrfc = surface(20*log10(Fmag));
set(hsrfc,'EdgeColor','none');
colorbar
caxis([ -20 80 ])
set(hsrfc,'ZData',fftshift(hsrfc.ZData));
set(hsrfc,'CData',fftshift(hsrfc.CData));
set(hsrfc,'XData',-0.5:fstep:0.5-fstep);
set(hsrfc,'YData',-0.5:fstep:0.5-fstep);
xlabel('F_x (\times\pi rad/sample)')
ylabel('F_y (\times\pi rad/sample)')
view([ -15 30 ])
zlim([ -20 80 ])

入力 X と出力 Y の周波数特性を比較してみて欲しい。どのようなことに気が付くだろうか？

直流におけるピークがなくなる。
水平方向の高域に減衰が見られる。

ということに注意して観察して欲しい。

[ トップ ]

二次元フィルタの周波数応答

二次元線形フィルタによる周波数特性の変化は、一次元の場合と同様に、フィルタの周波数応答により確認できる。

何故ならば、空間領域での畳込み演算は

$y[n_y,n_x] = h[n_y,n_x] \ast x[n_y,n_x] \ \stackrel{\mathrm{DSFT}}{\longleftrightarrow}\ Y(e^{j\omega_y},e^{j\omega_x}) = H(e^{j\omega_y},e^{j\omega_x})X(e^{j\omega_y},e^{j\omega_x})$

のように周波数（DSFT: 離散空間フーリエ変換）領域では積演算に対応するためである。ここで、

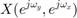$X(e^{j\omega_y},e^{j\omega_x})$ : 入力の周波数特性
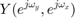$Y(e^{j\omega_y},e^{j\omega_x})$ : 出力の周波数特性
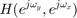$H(e^{j\omega_y},e^{j\omega_x})$ : フィルタ係数（インパルス応答）の周波数応答

である。

フィルタ係数 $$ h[n_y,n_x] $$ の周波数応答は freqz2 関数により確認できる。

figure(5)
freqz2(H)

振幅応答を確認すると、直流と水平方向の高周波数成分に対する減衰特性をもち、垂直方向については帯域通過特性をもつことが確認できる。

なお、

$H(e^{j\omega_y},e^{j\omega_x}) = \sum_{n_x=-\infty}^{\infty} \sum_{n_y=-\infty}^{\infty} h[n_x,n_y]e^{-j\omega_y n_y}e^{-j\omega_x n_x}$

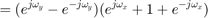
$= (e^{j\omega_y} - e^{-j\omega_y})(e^{j\omega_x} + 1 + e^{-j\omega_x})$

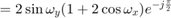
$= 2\sin\omega_y(1 + 2\cos\omega_x)e^{-j\frac{\pi}{2}}$

より、

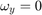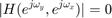
$\omega_y = 0$ で、 $|H(e^{j\omega_y},e^{j\omega_x})| = 0$
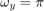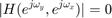
$\omega_y = \pi$ で、 $|H(e^{j\omega_y},e^{j\omega_x})| = 0$
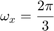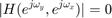
$\omega_x = \frac{2\pi}{3}$ で、 $|H(e^{j\omega_y},e^{j\omega_x})| = 0$
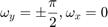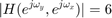
$\omega_y = \pm\frac{\pi}{2}, \omega_x = 0$ で、 $|H(e^{j\omega_y},e^{j\omega_x})| = 6$

となることが確認できる。

[ トップ ]

演習課題

課題2-1. 水平微分フィルタ

フィルタ係数 $$ h[n_y,n_x] $$ として配列

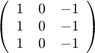
$\left(\begin{array}{ccc} 1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1 \\ \end{array}\right)$

（水平微分の離散近似フィルタ）を用意し、画像ファイル cameraman.tif のグレースケール画像に対して線形フィルタ処理を施し、処理結果を画像ファイル cameramangradx.tif に保存せよ。（負の値を考慮して、値0.5 によりかさ上げすること）。

また、フィルタの周波数特性をグラフで確認せよ。

(処理例）

課題2-2. 勾配の大きさと偏角

垂直微分フィルタ出力 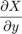$\frac{\partial X}{\partial y}$ と水平微分フィルタ出力 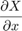$\frac{\partial X}{\partial x}$ から、

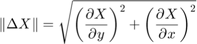
勾配の大きさ : $\|\Delta X \| = \sqrt{ \left(\frac{\partial X}{\partial y}\right)^2 +\left(\frac{\partial X}{\partial x}\right)^2}$
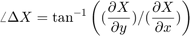
勾配の方向　 : $\angle \Delta X = \tan^{-1} \left((\frac{\partial X}{\partial y})/( \frac{\partial X}{\partial x})\right)$

を計算し、処理結果をそれぞれ画像ファイル cameramangradmag.tif と cameramangradang.tif に保存せよ。ただし、勾配の方向については、値の範囲を 0 から 1 に換算すること。

(処理例）

Part1 | メニュー | トップ | Part3

EmbVision チュートリアル（２）

Contents

一次元信号の周波数特性

一次元信号のフィルタリング

一次元フィルタの周波数応答

二次元信号の周波数特性

二次元信号のフィルタリング

二次元フィルタの周波数応答

演習課題